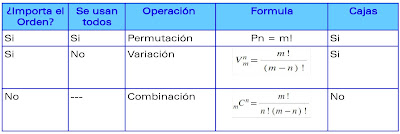
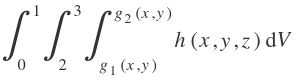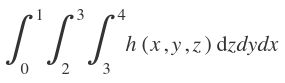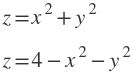La Notación
En los apuntes, se usa la extraña notación de:
FL es flotante
Punto Flotante
El PF es un concepto derivado de la notacion cientifica, y su uso en computacion o calculadoras, basicamente, significa que hay diferentes notaciones, para un numero dado, y el punto flotante, nos sirve para usar la notacion que mas nos sirva, recorriendo el punto a donde nos convenga.
Asi, supongamos que tenemos el numero 0.012345, podemos representarlo de las siguientes formas:
0.0012345 x 10-1 Base 10, p=7
1.2345 x 102 Base 10, p=4
Asi podemos operar con el como mas nos convenga, podemos unificar notaciones, como transformar medidas de centimetros a metro o a kilometro, o visceversa, y operar todo ordenadamente, asi supongamos que queremos sumarle a un metro un centimetro, primero normalizamos todo:
1 metro = 100 centimetros
O en notacion de punto flotante
1 m = 100 cm = 1 x 102 cm
1 x 10 2 cm + 1 x 100 cm = 100 cm + 1 cm = 101 cm
El ejemplo se ve trivial, pero su verdadero poder, es cuando estamos manejando cifras o muy grandes o muy pequeñas, asi 5x10-23 es mas facil de escribir que escribir los 23 ceros y cuando lo operamos con cantidades cuanticas muy semejantes, es mas conveniente operar con notacion cientifica, (llamada punto flotante por alguna extraña razon en los apuntes)
Asi en Relatividad tenemos la velocidad de la Luz: 300000000 m/s, lo que es mas facil de escribir como 3x108 m/s y cuando haces calculos de Relatividad, con raices cuadradas y toda la cosa, es mas comodo manejar todo con puntos flotantes (notacion cientifica)