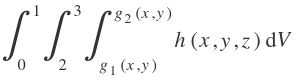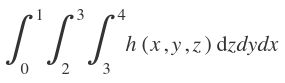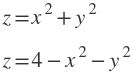La construccion de la Integral triple es como la doble, tenemos que basarnos en una construccion geometrica, y hay que hacerlo con cuidado, porque ahora los limites dependen de dos funciones, en la forma:
Como se ve, la integral interior, depende de dos funciones, la intermedias de una y la exterior debe de ser numerica, en este caso en particular tome los limites como dzdydx, por claridad, pero pueden tomarse en el orden que consideremos mas eficiente, dxdydz, dydzdx, etc.CUBO
Integremos sobre el cubo unitario de la figura, en el que:
PASO 1
Limites x,y
Proyectar sobre el eje xy
Esto nos produce un cuadrado:
Como se ve, es evidente que:
x∈[0,1]
y∈[1,2]
Por lo que ya tenemos los limites de integración para las integrales externa e intermedia
Por lo que nuestra integral quedaria:
EJEMPLO 2
Entre dos funciones
Ahora supongamos que deseamos calcular el volumen entre las funciones:
Notese que una cosa muy diferente son las Regiones en donde calcularemos la integral, y otra la funcion a integrar, que para evitar confusiones, la he llamado h(x,y,z) y no la especificare, porque no es importante para la construccion geometrica.
Esto nos define dos paraboloides, cuya interseccion se ve en la figura, una circunferencia:
PASO 1
Escoger el orden de Integracion
En este caso elijo dzdxdy, porque dado una (x,y), es facil darse cuenta donde comienza y donde acaba la z asociada a ella, empieza en el paraboloide inferior y termina en el superior (notese que solo es necesario escribir las ecuaciones en el respectivo lugar de la integral)
Asi mi integral triple quedaria:
Paso 2
Proyeccion sobre el eje xy
Lo que nos interesa es la proyeccion en el plano xy
 |
| La figura morada, es la sombra de la interseccion |
El calculo de la interseccion es:
PASO 3
Limites para x,y
Para todo valor de x, se ve que el valor va de la parte inferior de la circunferencia a la superior, como no podemos escribir la ecuacion de la circunferencia en la integral (son dos variables)=, despejamos y en funcion de x, y escribimos esto en los liumites, notese que cada semicirculo tendria asi, su propia ecuacion, que solo depende de x:
Asi que
De la inspeciión de la figura, se ve que x va de menos raiz de dos a raiz de dos, esto es delos extremos radio de la circunferenciaLo que significa que la integral dzdydx.quedarian.
Para este ejemplo me he basado en la clase 25 del Curso de Calculo Multivariacional del MIT:
NOTAS:
Esta es una de las posibles iteraciones, la proyeccion podria hacerse con los ejes xz o yz, se elige la que nos de los limites mas claros o bien, que pueda darnos una funcion de integracion mas manejable.
Es muy importante notar el orden de los limites de integracio:
- Para la integral interior, la funcion es maximo de 2 variables
- Para la intermedia, la funcion es maximo de una variable
- Para la exterior, solo puede haber valores numericos
- Si la variable de la interior es z, los limites deben estar en funcion de x e y
- Si la variable intermedia es y, entonces los limites deben de estar en funcion de x
- Y correspondientemente, en cada variable, le corresponde cierto orden de limites y diferenciales.