Socioeconomicas Actividad 3, Unidad 1

¿Qué sectores económicos están presentes en mi estado?

¿Cuál es el más representativo?

¿En qué sector económico identifico trabaja la mayoría de la población?

The Ascent of Money: Socieconomicas

Para Macroeconomia

Ángel, estudiante de Matemáticas

Les presentó a Ángel mi ayudante en el curso:

No se separa de mí mientras estoy en la Computadora, así que prácticamente ha tomado todo el curso desde el Propedéutico.

Introducción al Pensamiento Matemático, Unidad 1, actividad 1

1. Revisa el contenido del video que se encuentran en el apartado: recursos de apoyo
2. Ingresa al foro y realiza una intervención en la cual:
   • Escribas con tus propias palabras las definiciones siguientes: proposición, premisa, conclusión y razonamiento
   • Escribas al menos dos ejemplos de proposiciones simples y dos ejemplos de proposiciones compuestas
   • Desarrolles un ejemplo de una oración que no sea proposición

PARTE I

Para esto voy a presentar primero esta imagen:

PROPOSICIÓN
Def.

En Matemáticas, una Oración compuesta de al menos tres elementos básicos, a la que se puede asociar un Valor de Verdad, los elementos son:

1. A o la Hipotesis
2. B o la Conclusión
3. Un conector Lógico, en este caso ENTONCES  ⇒

A y B son conjuntos, o algunos de sus elementos, definidos por cierta propiedad

El conector establece una Relación entre A y B, de tal forma que se forma una estructura lógica entre ellas.

La Proposición puede ser Verdadera o Falsa, dependiendo de esos tres elementos.

Ejemplos:

• Si tengo hambre, ENTONCES, como
• Solo si una mujer es hermosa ENTONCES tendrá oportunidad de ser mi novia
• Si f(x) es derivable ⇒  f(x) es continua
• Si f(x) es continua  ⇒  no necesariamente f(x) es derivable

PREMISA

Una premisa es una idea que antecede o es causante a otra, usualmente por medio de una acción

Def.
En Matemáticas se le denomina Hipótesis y es el planteamiento de una Proposición.

Ejemplo

La premisa de la Gallina es el Huevo
La premisa del matrimonio, es el noviazgo

Las premisas o hipótesis en Matemática de color rojo

Si una sucesión es creciente y acotada ENTONCES será convergente
Si un objeto no posee sustentación en un campo gravitatorio ENTONCES caerá en dirección del centro de gravedad

CONCLUSIÓN

Def.
El Resultado de una acción o pensamiento: en Matemáticas el fin lógico de la Hipotesis y las Argumentaciones, dependiendo del conector lógico.

Ejemplos en azul:

Sexo sin condón te puede arruinar la vida
El que a hierro mata, a hierro muere

En Matemáticas, de azul

• Si n ∊ℕ  ⇒  n > 0
• Si hay una partícula en un campo magnético cerrado  ⇒  Tendrá una órbita cerrada

RAZONAMIENTO

Def.
Procedimiento, por medio del cual se puede pasar de una Hipótesis a una Conclusión, por medio de Argumentos Lógicos.

Ejemplo:
Debo de llegar a una cita importante en menos de media hora, estoy en el DF,  a pocas cuadras, pero el trafico no se mueve, ENTONCES, debe de haber una manifestación, ENTONCES, tardan mas de media hora en pasar, ENTONCES, mejor me bajo y me voy caminando, ENTONCES puedo pasar a comprar una paleta con los vendedores que siempre acompañan las manifestaciones ENTONCES que sea de un sabor que no manche mi camisa blanca ENTONCES llego a mi cita caminando, a tiempo y disfrutando de una paleta.

Ejemplo de Matemáticas
Demostrar que:

Si f(x) es continua ⇒  f(x) no siempre es derivable

Si f(x) es continua ⇒ f(x) puede ser dibujada sin separar el lápiz del papel
                              ⇒ en particular puedo dibujar la siguiente gráfica:

                              ⇒ Es continua, pero si me fijo en los vértices marcados con rojo

                              ⇒ En esos puntos la Derivada no puede ser determinada, por lo que NO EXISTE

                              ⇒ f(x) no es derivable
                              ⇒  f(x) no siempre es es derivable

PARTE II
Ejemplos

Simples

1. Ángel es cariñoso
2. Ángel esta en el teclado
3. Veracruz es bello

Compuestas

1. Ángel esta en contra del uso de acento escrito en el español.
2. Cuando Ángel esta contento Canta, o bien si ángel esta Contento, ENTONCES canta
3. Si un numero es par, ENTONCES es divisible entre 2

La mejor forma de saber si una Oración es Compleja es ver si la podemos pensar de la forma:
Si ... Entonces ...

PARTE III

Oración que no es Proposición

El mar quieto, sutil, perenne de Veracruz

BIBLIOGRAFÍA

En realidad no use mucha en esta ocasión, casi todo lo saque de mi memoria de cuando estudié Física, pero si desean mucha información recomiendo:

COURANT, R. Introducción al Cálculo y al Análisis Matemático, VOl. 1, LIMUSA, México 1982

Ya saben yo uso el mexicanísimo sistema Baena, abajo Trump y su APA.

Socieconomicas, Semana 2

1. Investiga sobre las aportaciones de las matemáticas en la asignatura "Contexto Socioeconómico de México.
2. Con la información obtenida crea una infografía de acuerdo a la historia del autor, aportaciones matemáticas y hallazgos importantes
3. Ingresa al foro y presenta tu infografía al grupo. Espera a que un compañero pueda evaluarte y elije a otra persona para evaluar su trabajo.

Este es un enlace a mi Navmap, las infografías se me hacen muy planas e infantiles, y creo que es divertido agrgarles un poco de movimiento.

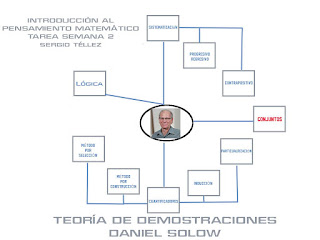
Introducción al Pensamiento Matemático, Semana 2

1. Investiga sobre un autor Matemático y sus principales aportaciones sobre la lógica proposicional, demostraciones y Teoría de conjuntos.
2. Con la información obtenida crea una infografía de acuerdo a la historia del autor, aportaciones matemáticas y hallazgos importantes
3. Ingresa al foro y presenta tu infografía al grupo. Espera a que un compañero pueda evaluarte y elije a otra persona para evaluar su trabajo.

La imagen es un Link al NAVMAP

Desarrollo Humano Timeline de las Matemáticas